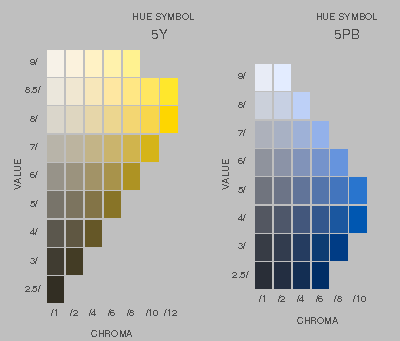
Equations for High Accuracy Conversion of CIE Luminance Factor to Munsell Value
Mikhail Semenov 2016-04-03
I have derived the following equations, which convert luminance factor to Munsell value with high accuracy – four correct digits after the decimal point. It is an improvement on the existing formula, proposed by McCamy[1], which has the maximum absolute error 0.0035.
Background
For some time, there has been a formula for conversion of the luminance factor to Munsell value [2], expressed as a fifth degree polynomial:
![]()
The range of V is [0; 10]. The range for Y is [0; 102.568].
The luminance factor is slightly higher than 100 because the reference white reflection was somewhat lower than that of the Munsell white color chip.
If on the other hand, if the absolute luminance factor is used (I will refer to it as Y100), which ranges from 0 to 100, the the following formula can be used [3]:
![]()
If conversion between these two factors is required the following formula can be applied:
![]()
Equations
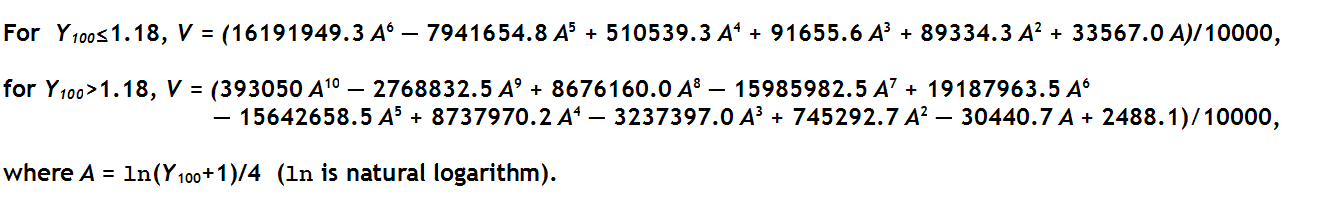
The absolute error in these equations in less than 0.00005; the relative error is about 0.0002 (0.02%).
Here is a program in C++ that demostrates the accuracy of this approximation:
MunsellValue.cppLicence Agreement
This program is free software. It is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
References
[1]. C.S McCamy. Munsell Value as Explicit Functions of CIE Luminance Functor. Color Research and Applications, 17(3), 205-207 (1992).
[2]. G. Wyszecki and W.S. Stiles. Color Science: Concepts and Methods, Quantitive data and Formulae, Second edition, John Wiley & Sons, 1982.
[3]. ASTM Standard D 1535-08. Standard Practice for Specifying Color by the Munsell System. American Society of the International Association for Testing and Materials, 2008.
Please, send your suggestions to the following address:
Created: 3 April 2016